php> print (time() - strtotime("+91"))/24/60/60;
4.0833333333333
php> print (time() - strtotime("+1"))/24/60/60;
0.33333333333333
php> print (time() - strtotime("-1"))/24/60/60;
0.25
php> print (time() - strtotime("-2"))/24/60/60;
0.20833333333333
php> print (time() - strtotime("-2"))/24/60/60;
0.20833333333333
php> print (time() - strtotime("+2"))/24/60/60;
0.375
Interesting. So I decided to make some graphs, of course. I eventually came up with this bit of code:
php -r '$range = 5000; function doit($i, $posneg) { $diff = (time() - strtotime("$posneg$i"))/24/60/60; if($diff > 10000) { $diff -= 15207; } print "$posneg$i,$diff\n"; } for($i=-$range;$i<=$range;$i++) { $posneg = ($i <= 0 ? "" : "+"); if($i == 0) { doit(0,"-"); } doit($i,$posneg); if($i == 0) { doit(0,"+"); } }' > phpstrtotime5000.csv
The $diff adjustment bit is because I was getting a lot of numbers that were waaaaay up around 15212, and a bunch around 1, but nothing in between, so I adjusted the big nubmers so they could be seen on the vertical scale. This is what I ended up with - the whole range, then zoomed in from -500 to 500: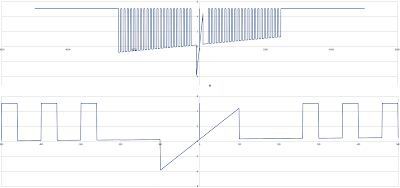 As I was putting this blog post together, I realized I could have done strtotime("-91",0) to just calculate from a timestamp of zero, so I tried that out:
As I was putting this blog post together, I realized I could have done strtotime("-91",0) to just calculate from a timestamp of zero, so I tried that out:
php -r '$range = 5000; function doit($i, $posneg) { $diff = strtotime("$posneg$i",0)/24/60/60; if($diff > 10000) { $diff -= 15207; } print "$posneg$i,$diff\n"; } for($i=-$range;$i<=$range;$i++) { $posneg = ($i <= 0 ? "" : "+"); if($i == 0) { doit(0,"-"); } doit($i,$posneg); if($i == 0) { doit(0,"+"); } }' > phpstrtotime5000_2.csv
This had the apparent effect of getting rid of all those weird outliers and replacing them with zeroes. That, combined with the number, made me realize that the 15212 number was in fact time()/24/60/60 - meaning that strtotime() probably returns zero regardless of the base time provided for those ranges. Here are my graphs from that run:
Now, I have no clue why strtotime() behaves like this. I know it's not defined how it should respond, but these numbers obviously have some kind of pattern, but I'm not sure what it is.
Some other tidbits: the last numbers that don't return zero are +/-2459, and the slope of the line is approximately -36.57 seconds with a y-intercept of precisely -8 hours. The little slope in the middle is in the range (-100,100), with a slope of exactly -1 hour, and a y-intercept of exactly -8 hours again. The zero sections occur every 100 values - the function is zero from [100n+60,100n+99] for positive numbers, [100n-60,100n-99] for negative numbers, |n| > 1. For |n| <=1 - (-200,200) - there is the aforementioned discontinuity, plus a slight change in slope outside the (-100,100) range. Outside that range - in the ranges (-200,-100] and [100,200) - the slope is -47.94 seconds, again with that y-intercept of -8 hours. "+0" and "-0" are both 0.33333 days, but "0" returns 0 days.
I can guess that the zeroes are related to minutes in an hour or seconds in a minute, with 60 being a factor there - something is defined for 0-59, but not for 60-99. The y-intercept appears to be related to the current hour/time of day - my first sampling was taken at 1:XX UTC (6:XX local time) and the second at 2:XX UTC (7:XX local time), and the y-intercept changed from -7 to -8.
For reference, I was running the first set of stats at approximately 1:49:30am UTC, Friday, August 26, and the second stats some time afterwards. I'm in Pacific time, currently GMT-7.
I'm not sure is the cause of all this weirdness, and I know it doesn't matter at all, but it is really interesting - maybe sometime I'll have the time to plumb through the code and figure it out. If anyone else wants to play with it, I've put my numbers in a Google Spreadsheet that you can check out and download if you want.
P.S. I had formerly run the numbers with the upper graph, and the results were the exact same slopes (36.57 seconds, 1 hour, just y-mirrored, but with a y-intercept of 7 hours. Odd, but probably significant.



No comments:
Post a Comment